本文为:ES聚合算法原理深入解读:深度优先算法(DFS)和广度优先算法(BFS)第二篇
深度优先算法(DFS)和广度优先算法(BFS):DFS 和 BFS 在 ES 中的应用(一)
深度优先算法(DFS)和广度优先算法(BFS):深度优先搜索算法(二)
深度优先算法(DFS)和广度优先算法(BFS):广度优先搜索算法(三)
2、深度优先搜索(Depth-First Search)
2.1 什么是深度优先算法
一句话导读:当你玩迷宫游戏的时候,你进入迷宫那一刻,右手摸着墙手不离开,不停前进,直至走出迷宫,此时你使用的就是深度优先搜索。
2.2 图的深度优先搜索
和树不同,图没有根节点,并且是可以回溯的,比如下图所示,为一个 11 节点的图搜索表示
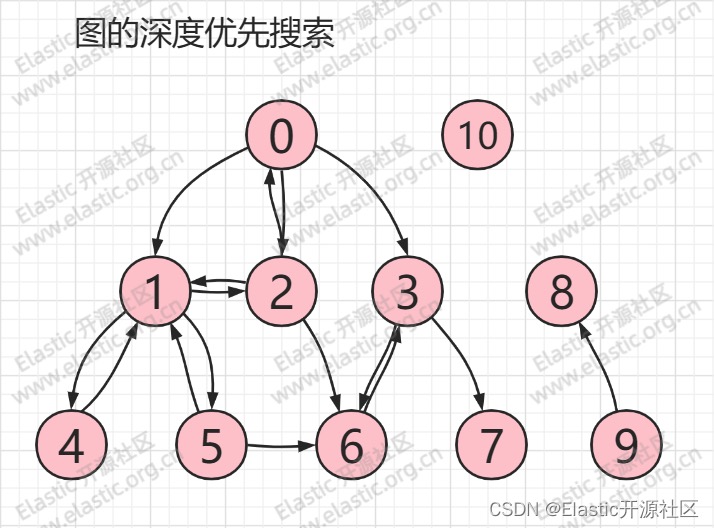
其中:
- **节点0** :包含三个出度,分别指向其三个邻接点,分别为`节点1、节点2、节点3`,同时`节点0`也是`节点2`的邻接点。
- **节点1**:包含三个邻接点,分别为`节点2、节点4、节点5`
- **节点2**:邻接点为`节点0、节点1、节点6`。
- **节点3**:邻接点为`节点6、节点7`。
- **节点4**:邻接点为`节点1`。
- **节点5**:邻接点为`节点1、节点6`。
- **节点6**:邻接点为`节点3`。
- **节点7**:没有任何邻接点,因为`节点7`的出度并没有指向任何节点。或者说其没有任何出度
- **节点8**:和`节点7`一样,没有任何邻接点
- **节点9**:邻接点为`节点8`。
- **节点10**:和`节点7`一样,没有任何邻接点。
2.3 邻接表
下图为 2.2 中图搜索所示图的邻接表形式。可以看到,节点7、节点8、节点10 是没有任何出度和邻接点的。
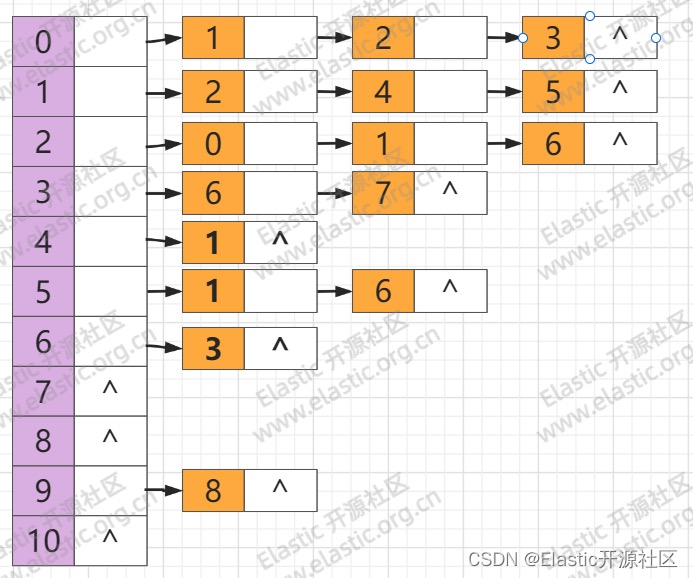
## 2.4 邻接矩阵
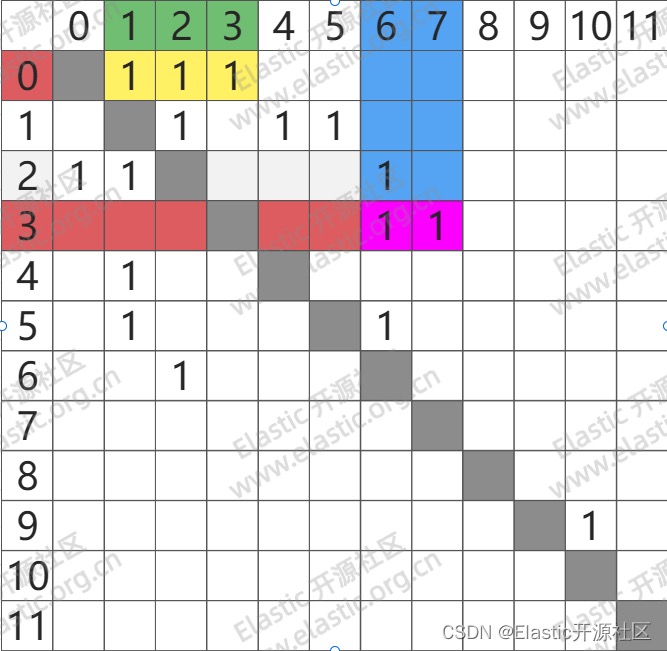
下图为 2.2 中图搜索所示`图`的`邻接矩阵`表示
其中,纵坐标表示 出度节点,横坐标表示 邻接点
比如,下图中:
- 节点0:邻接点为
节点1、节点2、节点3
- 节点3:邻接点为
节点6、节点7
## 2.5 图的深度优先搜索遍历过程
2.5.1 栈
图的深度优先遍历是靠栈来完成的,我们首先创建一个空栈

### 2.5.2 Visited数组

我们借助 Visited数组,来标识当前节点 n 是否被访问过,空值代表 false.
2.5.3 遍历序列
准备一个空的遍历序列,用来存放最终生成的访问元素。

### 2.5.4 遍历过程
首先,图是没有根节点的,我们可以以任何节点作为其起始节点,下面我就以`节点0`为起始节点为例,演示一下图的深度搜索过程。
第1步
节点0入栈
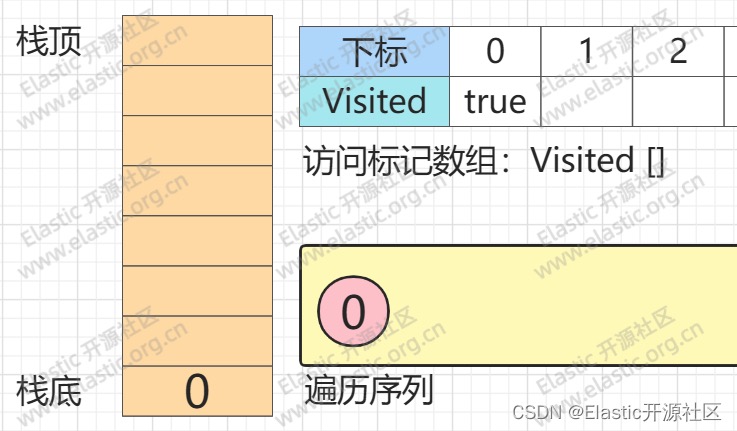
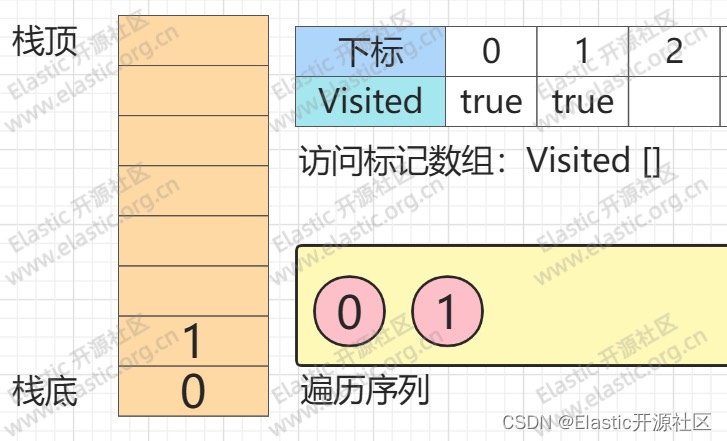
**第2步**
**`节点0`的第一个邻接点入栈**
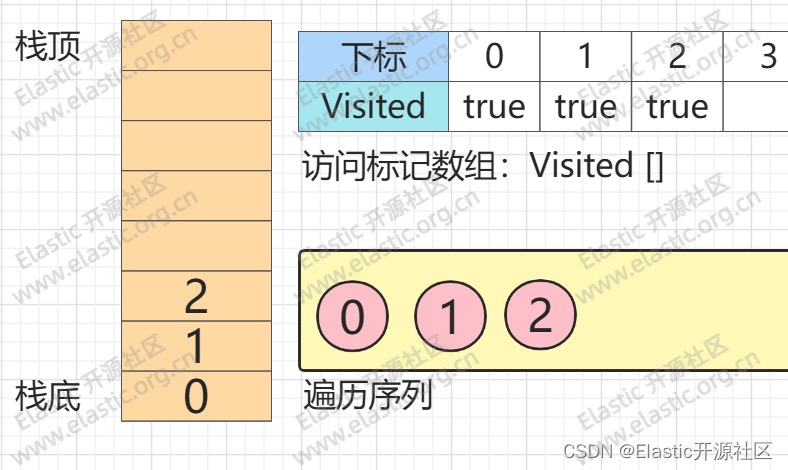
**第3步**
**`节点1`的第一个邻接点`节点2`入栈**
**第4步**
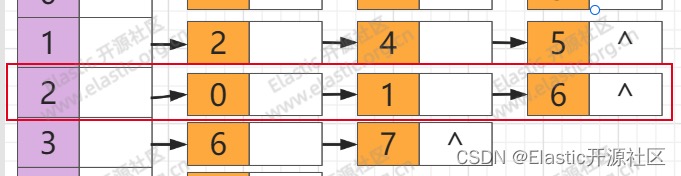
**`节点2`的第一个邻接点`节点0`入栈**,但是`节点0` visited = true,即已经被访问过,因此顺延`节点1`,同样`节点1`也被访问过,因此继续顺延值`节点6`,`节点6`入栈并标记访问
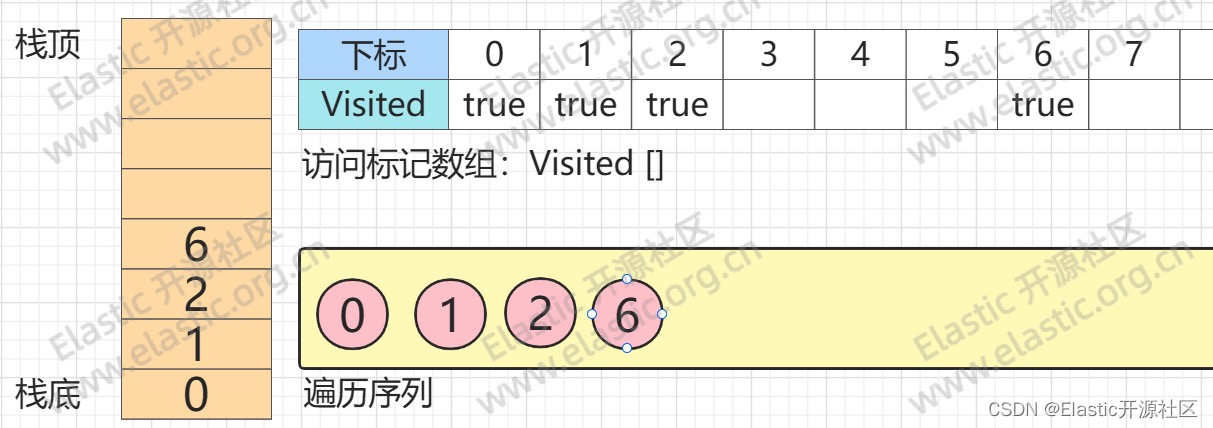
**第5步**
**`节点6`的第一个邻接点也是唯一一个邻接点:`节点3`入栈**
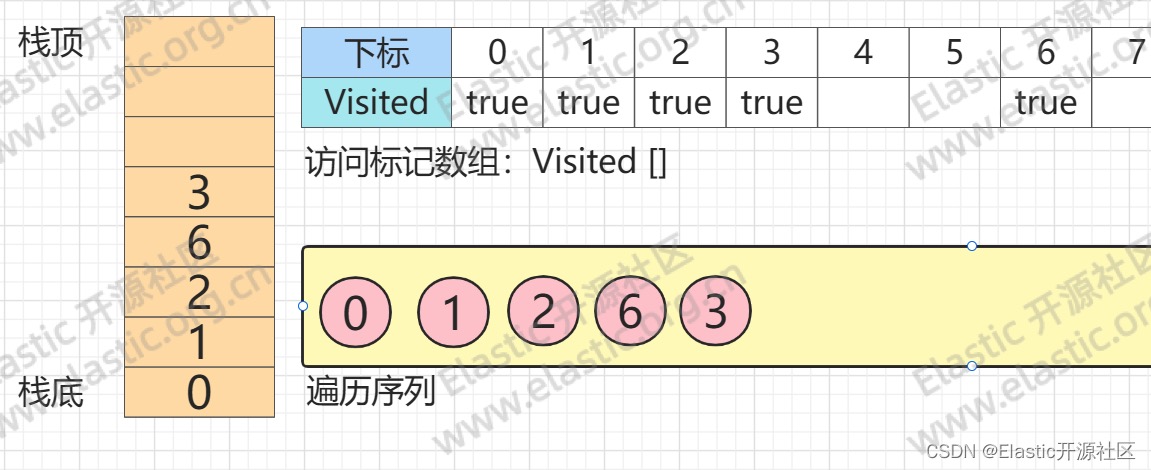
**第6步**
**`节点3`的第一个邻接点也是唯一一个邻接点:`节点7`入栈**

**第7步**
**`节点7`没有任何出度和邻接点,此时`节点7`出栈**,回溯至`节点3`

**第8步**
**`节点3`的唯一一个邻接点:`节点7`已经被访问,此时`节点3`的所有邻接节点均已访问,此时,`节点3`出栈,回溯至`节点6`**
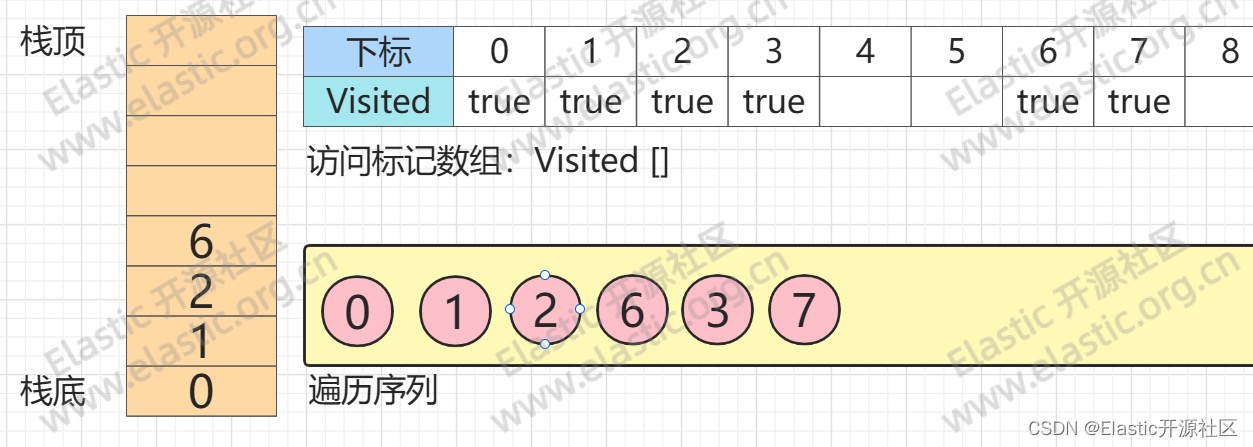
**第9步**
**同理,此时`节点6`的唯一一个邻接点:`节点3`已经被访问,此时`节点6`的所有邻接节点均已访问,此时,`节点6`出栈,回溯至`节点2`**
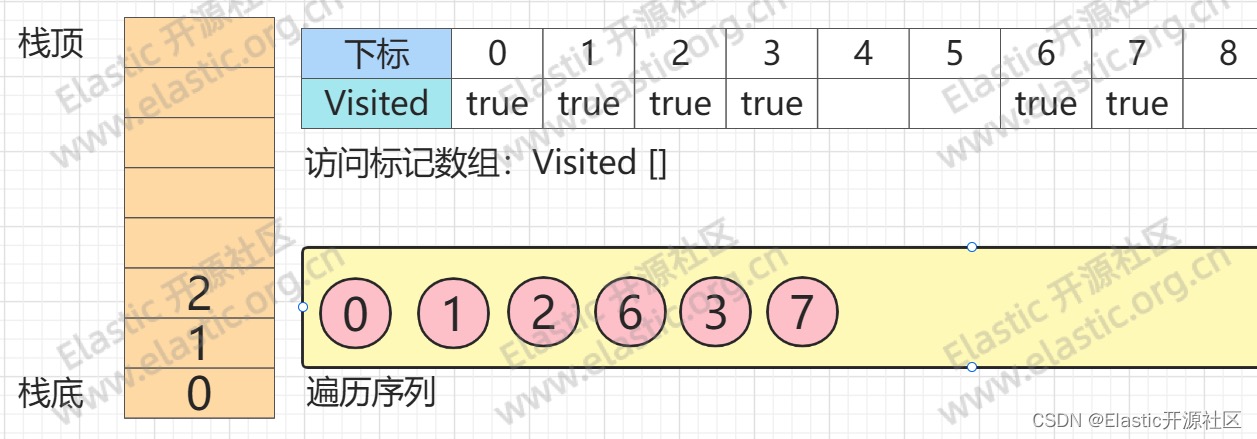
**第10步**
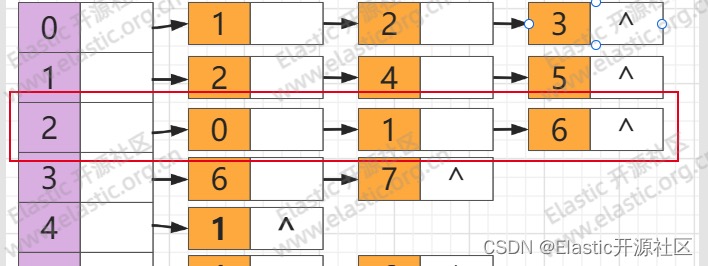
**此时`节点2`的三个邻接点:`节点0、节点1、节点6`均已被访问过,因此`节点2`出栈,回溯至`节点1`**

**第11步**
**此时`节点1`的三个邻接点:`节点2、节点4、节点5`其中`节点2`已被访问,因此`节点4`入栈**
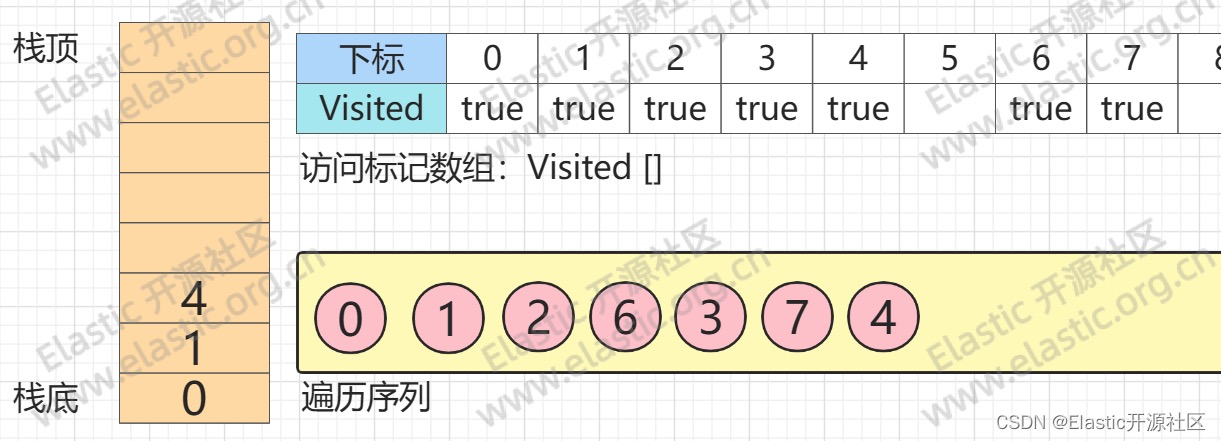
**第12步**
**以此类推,`节点4`出栈 => `节点5`入栈,并回溯至`节点1`,`节点1`所有邻接点均已访问。`节点1`出栈,回溯至`节点0`**
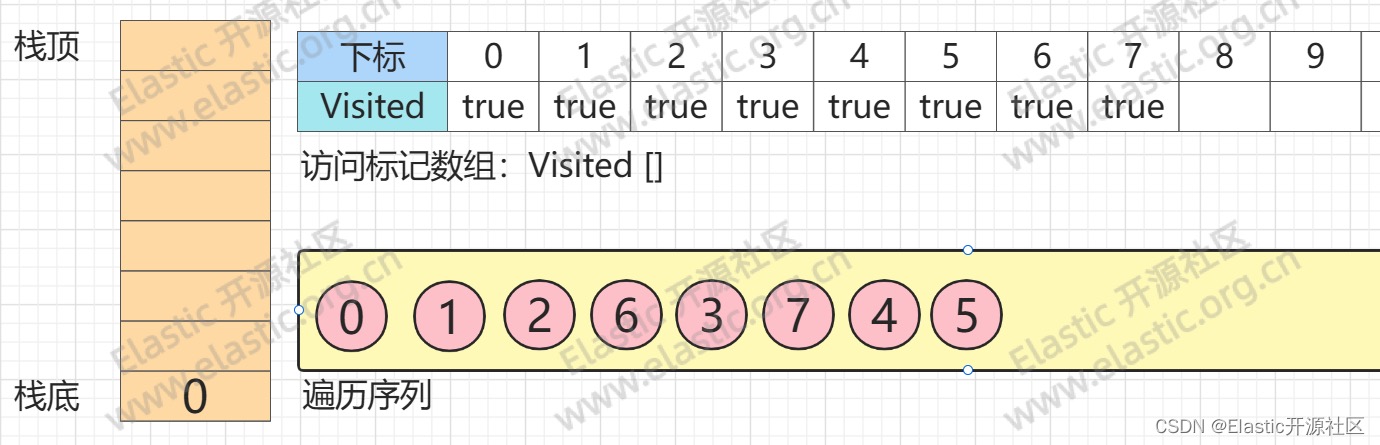
**第13步**
**此时,`节点0`的所有出度邻接点均已访问,`节点0`出栈,此时为空栈
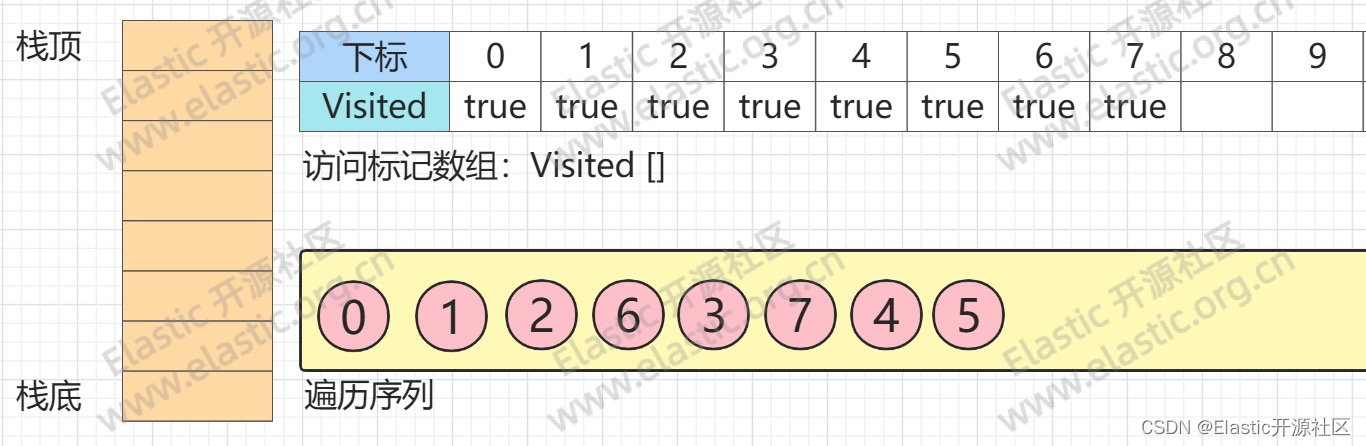
**第14步**
此时,`节点8`入栈,`节点8`所有邻接点均已访问,`节点8`出栈,而后,`节点9`入栈,而后马上出栈。以此类推,最后,`节点10`入栈,而后而后马上出栈,生成最终序列,如下图所示**
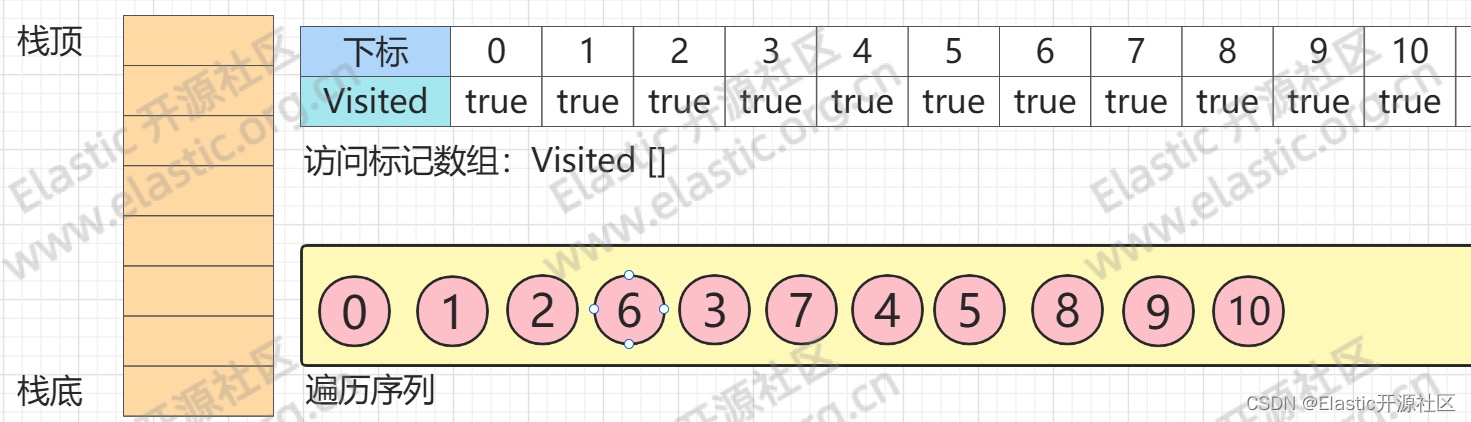
## 2.6 树的深度优先搜索
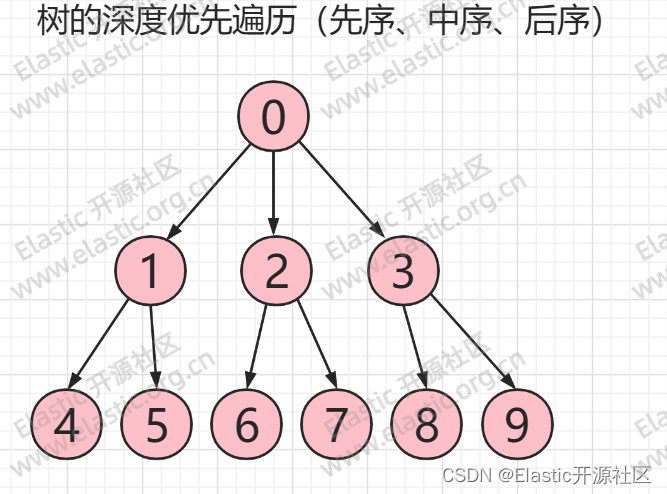
由上所述遍历过程,树的深度优先遍历序列如下图所示


























